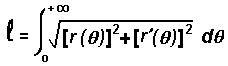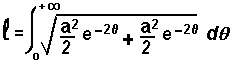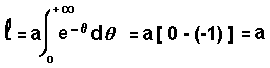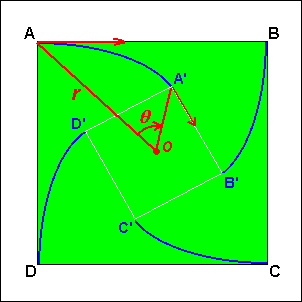
Compte-tenu des déplacements simultanés, les chiens A B C D forment à tout instant les sommets d'un carré qui est de plus en plus petit et en rotation autour du centre O. Quelle que soit la position A' du chien A, l'angle que fait le rayon vecteur OA' avec la tangente en A' à la trajectoire est constant et égal à 45°. La situation est identique pour les autres chiens. Zaftra vous expliquera (si vous y tenez !) que dans ce cas, la trajectoire est une spirale logarithmique d'équation (en coordonnées polaires ) :
L'élément dl de trajectoire vaut : La longueur totale de la trajectoire de chaque chien s'obtient en calculant l'intégrale : soit :
Ainsi, en fin de trajectoire, chaque chien a parcouru une longueur égale à a, côté du carré de départ. Note de Zaftra : il est intéressant de noter que les chiens tournent en rond indéfiniment avant de se rencontrer, bien que la distance parcourue soit finie !
Et maintenant, voici la solution, inventive, élégante, astucieuse, (ici, autre qualificatif de votre choix) de pfz : Pour prouver que la distance parcourue est égale à a, pas besoin de sortir l'artillerie lourde avec des exponentielles et des intégrales à la mords-moi la queue (du chien) ; il suffit de bien regarder ce qui se passe pendant les déplacements des chiens A et B. En effet, on peut constater qu'à tout instant, la direction du mouvement du chien B est perpendiculaire à la direction du mouvement du chien A. Donc, pendant que A avance vers B, B ne s'éloigne jamais de A. Quand le chien A aura rejoint le chien B, il aura parcouru exactement la distance de départ AB = a Bravo et merci, pfz ! (envoyez vos commentaires et félicitations ici )

Haut de la page

Retour au Problème

Vers Sommaire

Vers Accueil