PROBLEME n° 17
Le "gnomon tridimensionnel"

Vous vous souvenez du "Coup du Gnomon" ? ( cf. pb n°6 )

Il fallait démontrer que "le carré de la somme est égal à la somme des cubes" :

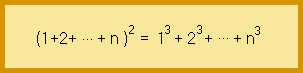
Aujourd'hui, les vieux "#@@!!¤§" du groupe ZAFTRA vous proposent perfidement de démontrer l'égalité

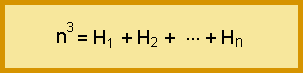
où H₁, H₂, ..., H_n sont les nombres hexagonaux de rang 1, 2, ..., n.

Rappel pour les nuls (et pour pfz !) :
Les nombres hexagonaux sont les nombres qui permettent des arrangements hexagonaux dans le plan (comme le montre
la figure ci-dessous). A partir de H₁ = 1, on peut déduire les autres nombres H par la formule H_n+1 = H_n + 6n . Ainsi :

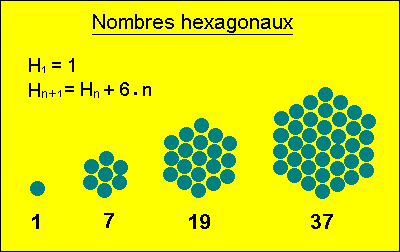
Avec le sens critique qui vous caractérise, cher visiteur, vous devriez vous demander, avant de vous lancer dans des calculs forcément laborieux, à quoi peut bien servir cette égalité ?
Elle ne sert strictement à rien !

En revanche, la démonstration que ZAFTRA va vous présenter est intéressante.
La clé de l'énigme, c'est le "Gnomon tridimensionnel" !... Mais je n'en dis pas plus !
A vous de chercher ou de vous précipiter vers la !